Modell der Ortsabhängigkeit

Ich betrachte einen Kristall mit quadratischem Querschnitt $4s2$, wie er in der Abbildung 40 gezeigt wird. Er soll beliebig lang sein und das eine Ende soll den effektiven Kristall des Expperiments genügend gut beschreiben. Die Lichtquelle befinde sich auf der langen Schwerpunktsachse des Kristalls $(x$₀,0,0).

  
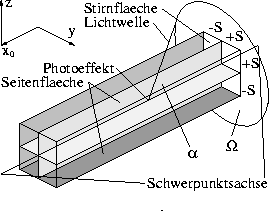
Abbildung 40: Definition der Kristallgeometrie. Ein Photoeffekt erzeugt Licht, welches unter dem Winkel $\alpha$ zwischen der Schwerpunktsachse und der Lichtwelle auf die Ebene der Kristallstirnfläche trifft. Aufgrund der rotationssymetrischen Anordnung spannt das in dieser Ebene betrachtete Licht den Raumwinkel $\Omega$ auf.

Die Reflexionsbedingungen sind gegeben durch den kritischen Winkel $\alpha$_krit=π/4 zwischen der Lichtwelle und der Schwerpunktsachse. Trifft die Lichtwelle unter einem Winkel _krit auf eine Kristalloberfläche, so wird sie wiederum unter dem Winkel $\alpha$ reflektiert. Hingegen werden Lichtwellen für Winkel $\alpha >\alpha$_krit durch die Kristalloberfläche hindurch gehen. Zusammen mit der rechteckigen Querschnittsfläche des Kristalls führen diese Annahmen zu folgenden Voraussetzungen.

• $\alpha >\alpha$_krit⇒ Die Lichtwelle erfährt eine Transmission durch die Kristalloberfläche spätestens nach der ersten erfolgten Reflexion ($\Rightarrow$ trivialer Fall).
• _krit⇒ Die Lichtwelle wird nach endlich vielen Reflexionen an die Stirnfläche des Kristalls gelangen und durch diese eine Transmission erfahren ($\Rightarrow$ interessanter Fall).

Ich will ausschliesslich den interessanten Fall behandeln. Seine Voraussetzungen stellen sogleich eine Bedingung auf. Für die Abbildung 40 muss stets gelten $\Omega \pi /2$ sr $\Rightarrow R=x$₀. Nimmt man den Photoeffekt als den Ursprung der betachteten Lichtwelle, so spannt diese einen Kugelsektor vom Radius $2R$ und dem Raumwinkel $\Omega$ auf.
Beginne ich die Betrachtungen mit der Lichtquelle bei $x$₀=0 und verschiebe diese allmählich gegen $x$₀→&inf;, so bauen sich durch den gewählten Lichtkegel sukzessive rechteckige zur Stirnfläche planparallele Reflexionsgebiete der Fläche $4s2$ auf, für welches die Abbildung 41 ein zweidimensionales Beispiel in der $x$₀-$z$-Ebene darstellt.

Für den dreidimensionalen Fall ist die $y$-$z$-Ebene in der Abbildung 42 dargestellt. Der gewählte Lichtkegel hat per Definition einen maximalen Radius $R=x$₀.

      
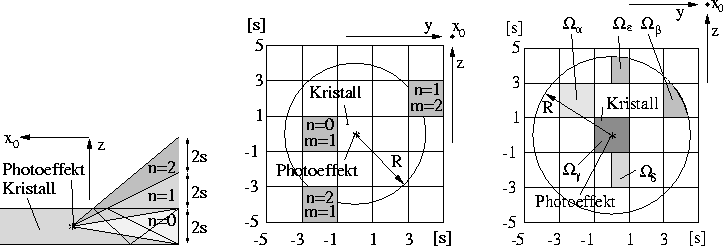
Abbildung 43: Illustration zu den unterschiedlichen Reflexionsgruppen und deren dazugehörigen Raumwinkelgruppen.
Abbildung 42: Zweidimensionale Darstellung von Reflexionsbeispielen in der $y-z$-Ebene. Dabei sind $n$ die Anzahl Reflexionen in der $x$₀-z-Ebene und $m$ die Anzahl Reflexionen in der $x$₀-y-Ebene.
Abbildung 41: Zweidimensionale Veranschaulichung der Projektion auf die Ebene der Stirnfläche von drei verschiedenen Reflexionsgebieten.

Betrachtet man die Projektionsebene, welche mit der KristallstirnflÄche zusammenfällt, werden die quadratischen Reflexionsgebiete in der Abbildung 43 vom Zentrum $(0,0,0)$ aus kreisförmig mit dem Radius $R$ aufgebaut. Im folgenden möchte ich kurz die jeweiligen Raumwinkelelemente analytisch herleiten (Ref.[19]). Dabei werde ich, wie in der Abbildung 43 dargestellt, die einzelnen Raumwinkelgruppen $\Omega$_ζ(x₀,s) mit $\zeta =\alpha ,\beta ,\gamma ,\delta ,\epsilon$ einzeln berechnen und zuletzt in einem enzigen Ausdruck vereinen. $\Omega$_α repräsentiert eine Raumwinkelgruppe, welche die gesamte Stirnfläche des Kristalls abdeckt.

  
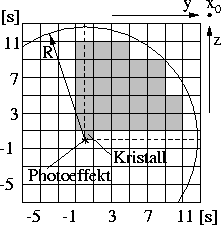
Abbildung 44: Illustration zur Symmetriesituation. Die schraffierte Fläche stellt einen Viertel der gesamten Raumwinkelsituation dar. Deshalb genügt es, die Raumwinkelgruppen dieser schraffierten Fläche zu berechnen.

Man kann aus geometrischen Überlegungen sagen, dass die Elemente dieser Raumwinkelgruppe innerhalb des Lichtkegels mit Radius $R$ liegen. $\Omega$_β steht für eine Raumwinkelgruppe, deren Elemente auf dem Rand des Lichtkegels mit Radius $R$ liegen. Das reflexionslose Element stellt der Raumwinkel $\Omega$_γ dar. Die letzten beiden Gruppen $\Omega$_δ und $\Omega$_ε sind symmetriebedingte Spezialfälle der ersten beiden Gruppen.

  
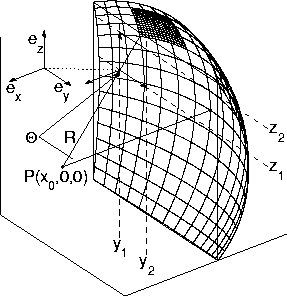
Abbildung 45: Ansicht der Raumwinkelgeometrie.

Ich beginne mit der Berechnung von $\Omega$_α(x₀,s). Aus Symmetriegründen, wie es die Abbildung 44 illustriert, genügt es, für einen Viertel aller Reflexionsgebiete die Raumwinkel zu berechnen. Gemäss der Abbildung 45 benötige ich $dye$_y; $dze$_z und den Winkel $\Theta$, um das Raumwinkelelemend $d\Omega$_α zu beschreiben. Dabei können $y$ ($\Leftarrow y=ye$_y) und $z$ ($\Leftarrow z=ze$_z) frei gewählt werden.

Damit erhalte ich für $\Theta$ eine Funktion $\Theta =\Theta (x$₀,y,z) mit den Variablen $x$_o, $y$ und $z$. Analog gilt für den Raumwinkel die Abhängigkeit $\Omega$_α=Ω_α(x₀,y,z). Vorerst benötige ich $cos(\Theta )$ und den Radius $R$.

$R=x$₀e_x+ye_y+ze_z |R|² = x₀²+y²+z² cos(Θ) = e_x{R|R|} = e_x{(x₀e_x+ye_y+ze_z)x₀²+y²+z²} = {x₀x₀²+y²+z²}

und daraus folgt für das Raumwinkelelement $d\Omega$_α

$d(d\Omega$_α) = {cos(Θ)|R|²} dz dy = {x₀{(x₀²+y²+z²}^(3/2)} dz dy.

Der Raumwinkel $\Omega$ ergibt sich durch zweifache Integration über die Strecken $|y|=y$₂-y₁ und $|z|=z$₂-z₁.

$\int d\{[\int d\Omega$_α} = ∫y₁y₂∫z₁z₂{cos(Θ)|R|²} dz dy = ∫z₁z₂∫y₁y₂{x₀{(x₀²+y²+z²}^(3/2)} dz dy

Im Ausdruck (12) habe ich mit den jeweiligen Integrationsbereichen angedeutet, dass ich die Integrale ganz allgemein lösen und dann spezifische Integrationsgrenzen setzen möchte. Gleichung (12) lässt sich ein erstes mal Integrieren.

$\Omega$_α(x₀,y₁,y₂,z₁,z₂) = x₀∫z₁z₂{y₂(x₀²+z²)x₀²+y₂²+z²} dz - x₀∫z₁z₂{y₁(x₀²+z²)x₀²+y₁²+z²} dz

Für die zweite Integration benötige ich folgende Substitutionen:

$w\equiv \{zz2+x$₀²+y₁²} v ≡ {zz²+x₀²+y₂²}

Da mit $w$ und $v$ analog zu rechnen ist, genügt es für die weiteren Überlegungen, nur noch $w$ zu betrachten. Ich setze vorübergehend $y$₁≡y.

$(5)\Rightarrow w2(z2+x$₀²+y²) = z² ⇒ z² = {w²(x₀²+y²)1-w²} ⇒ z = {wx₀²+y²1-w²}.

Woraus sich das Differential $dz$ ergibt

$dz=x$₀²+y²{[{11-w²}-{12}{w(-2w){(1-w²}^(3/2)}}dw = x₀²+y²&thicksp;{1-w²+w²{(1-w²}^(3/2)}&thicksp;dw = {1{(1-w²}^(3/2)}&thicksp;dw.

Weiter ist

$x$₀²+z² = {x₀²(1-w²)+w²(x₀²+y²)1-w²} = {x₀²+y² w²1-w²} x₀²+y²+z² = {x₀²+y²w²+y²-y²w²1-w²} = {x₀²+y²1-w²}.

Damit schreibt man den Raumwinkel $\Omega$_α in folgender Form:

$\Omega$_α(x₀,y,z₁,z₂) = x₀ y∫w₁w₂{1-w²(1-w²)x₀²+y²x₀²+y²(x₀²+y²w²){(1-w²}^(3/2)}&thicksp;dw = x₀ y∫w₁w₂{dw(x₀²+y²w²)} = {x₀y}∫w₁w₂{dw{x₀²y²}+w²}

Für dieses Integral existiert ebenfalls ein analytischer Ausdruck.

$\Omega$_α(x₀,y,z₁,z₂) = {x₀y}{[{24{x₀²y²}}arctan{({2w₂4{x₀²y²}}}} - {x₀y}{[{24{x₀²y²}}arctan{({2w₁4{x₀²y²}}}}

Nun werde ich die Substitutionen (5) wieder rückgängig machen. Das führt mich auf

$\Omega$_α(x₀,y,z₁,z₂) = arctan{({y z₂x₀x₀²+y²+z₂²}} - arctan{({y z₁x₀x₀²+y²+z₁¹}}.

Um die exakte Form von $\Omega$_α nun angeben zu können, muss ich in der Gleichung (12) $y\equiv y$₁ und $y\equiv y$₂ nacheinander einsetzen. Somit lautet der effektive Raumwinkel, betrachtet über die Strecken $|y|=y$₂-y₁ und $|z|=z$₂-z₁:

$\Omega$_α(x₀,y₁,y₂,z₁,z₂) = arctan{({y₂ z₂x₀x₀²+y₂²+z₂²}} - arctan{({y₁ z₂x₀x₀²+y₁²+z₂²}} - arctan{({y₂ z₁x₀x₀²+y₂²+z₁²}} + arctan{({y₁ z₁x₀x₀²+y₁²+z₁²}}

Da ich den Raumwinkel in der Form $\Omega$_α = Ω_α(x₀,s) haben will, muss ich die Integrationsstrecken $|y|$ und $|z|$ in Abhängigkeit von möglichen Reflexionen bringen. Ich suche beispielsweise den Raumwinkel $\Omega$_α(x₀,n) für die $n-te$ Reflexion an den Seitenflächen unter den Bedingungen

• Es wird nur das Licht betrachtet, welches unter dem gesuchten Raumwinkel $\Omega$_α(x₀,n) ausgesandt wird.
• Die auszulesende Stirnfläche muss durch den gesuchten Raumwinkel $\Omega$_α(x₀,n) vollständig abgedeckt sein.
• Jeder betrachtete Lichtstrahl muss genau n mal an einer Seitenfläche unter dem Winkel $\alpha \alpha$_krit = π/4 reflektiert werden, bevor er auf die durch den Photmultiplier auszulesende Stirnfläche trift.

Der Veranschaulichung wegen zeige ich die Abbildung 46, in welcher für die 2. und 3. Reflexionsordnung jeweils ein Beispiel für einen Raumwinkel dargestellt ist.

  
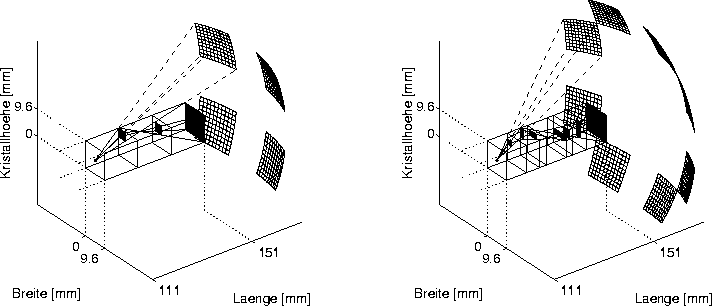
Abbildung 46: Raumwinkelillustration für Reflexionen 2. und 3. Ordnung. Die schraffierten Flächen auf der Projektionskubeloberfläche sind innerhalb jeder Reflexionsordnung kongruent.

Für den reflexionslosen Fall, also für das direkt einfallende Licht, vereinfacht sich die Gleichung (13). Die identischen Integrationsstrecken $|y|=y$₂-y₁=|z|=z₂-z₁ kann ich angeben als $s\equiv y$₂=-y₁=z₂=-z₁ wobei $s$ gerade die halbe Querschnittslänge des Kristalls ist. Damit wird Gleichung (13) zu

$\Omega$_α(x₀,s,n=0) = 4arctan{({s²x₀x₀²+2s²}}

Zur Überprüfung betrachte ich den Fall, dass die Lichtquelle ($\Leftarrow$ Photoeffekt) genau in der auszulesenden Stirnfläche positioniert ist. Damit ist die Bedingung $x$₀=0 gesetzt. Ich erwarte, dass der Raumwinkel einer Halbkugel entspricht. Der Ausdruck (14) wird dadurch zu

$lim$x₀→0Ω_α(x₀,s,n=0) = limx₀→04arctan{({s²x₀x₀²+2s²}}= 2π

was genau den Erwartungen entspricht.
Der eben konstruierte Fall macht physikalisch wenig Sinn, da die Lichtquelle genau in der Stirnfläche liegt. Ganz allgemein soll durch die Reflexionsanzahl $n$ eine eindeutige Randbedingung für die Lichtquellenposition $x$₀ definiert werden. Anders formuliert kommen für jeden Abstand $x$₀ nur diskrete definierte Reflexionen $n$ in Frage. Beim reflexionslosen Fall $n=0$ beispielsweise gilt

$Fall\; a)0x$₀s Fall b) sx₀2s Fall c) 2sx₀

Im Fall a) wird nicht die gesamte Stirnfläche durch den Raumwinkel abgedeckt. Im Fall b) wird mindestens der in die Stirnfläche projzierte Innkreis des Radius $(x$₀=)R=s abgedeckt, nicht aber die gesamte Stirnfläche $4s2$. Im Fall c) wird in der Tat die ganze auszulesende Stirnfläche durch den Raumwinkel abgedeckt. Demnach lautet die exakte Beschreibung für die reflexionslose Situation:

$\Omega$₀(x₀,s) = 4arctan{({s²x₀x₀²+2 s₂²}} &quad;mit&quad;x₀2s

Im weiteren will ich den Raumwinkel $\Omega$_α(x₀,n,m,s) in Abhängigkeit der beiden Reflexionsparameter $n$ und $m$ bringen. Dazu möchte ich die beiden Parameter kurz definieren.
Definition 1: $n\; \equiv$ Gesamtzahlzahl der Reflexionen an einem planparallalen Seitenpaar und $m\; \equiv$ Gesamtzahlzahl der Reflexionen am senkrecht dazu ausgerichteten planparallalen Seitenpaar.
Weil es auf der Schwerpunktsachse $A\; =\; (x$₀,0,0) eine Reflexionssymmetrie über $\{\pi 2\}$ gibt, betrachte ich künftig nur noch den symmetrischen Ausschnitt von $\{\pi 2\}$. Die Abbildungen 42 und 44 haben dies bereits illustriert. Dabei gilt für $n$ und $m$

Die Integrationsgrenzen aus (13) werden gemäss der Abbildung (43) zu

$y$₁ = (2m-1)s y₂ = (2m+1)s z₁ = (2n-1)s z₂ = (2n+1)s

und damit wird Gleichung (13) zu

$\Omega$_α(x₀,s,n,m) = arctan{({(2m+1)(2n+1)s²x₀x₀²+{[(2m+1)²+(2n+1)² }s²}} - arctan{({(2m-1)(2n+1)s²x₀x₀²+{[(2m-1)²+(2n+1)² }s²}} - arctan{({(2m+1)(2n-1)s²x₀x₀²+{[(2m+1)²+(2n-1)² }s²}} + arctan{({(2m-1)(2n-1)s²x₀x₀²+{[(2m-1)²+(2n-1)² }s²}} mit&quad;x₀≥(2m+1)²+(2n+1)²s und&quad;n = 1,2,3,&ldots; und&quad;m = 1,2,3,&ldots;,n.

Mit der Konvention $[k]\in N$ sei eine natürliche Zahl kann ich den gewünschten Ausdruck für $\Omega$_α(x₀,s) endlich angeben. Es ist dabei $p$ der prozentuale Lichtverlust pro Reflexion.

$\Omega$_α(x₀,s) = 4∑_n=1^[k]∑_m=1^[l]p^(n+m)Ω_α(x₀,s,n,m) mit&quad;k={{x₀²-s²s²}+12} und&quad;l={{x₀²-(2n+1)²s²s²}-12}.

  
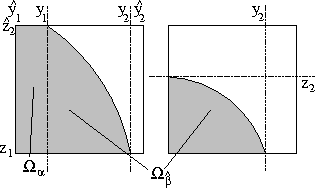
Abbildung: Zwei typische Beispiele für den Raumwinkel $\Omega$_β. Dieser ist die Summe aus dem bereits bekannten Raumwinkel $\Omega$_α und dem Raumwinkel $\Omega$_β.

Als nächstes werde ich den Raumwinkel $\Omega$_β(x₀,s) berechnen. Die Abbildung 47 illustriert die Besonderheoten dieses Raumwinkels. Zu diesem Zweck muss das aus der Gleichung (3) hervorgehende Doppelintegral gelöst werden

$\Omega$_β{(x₀,y₁,y₂,,z₁,R²-y²} = ∫z₁R²-y²∫y₁y₂{x₀&thicksp;dy&thicksp;dz(x₀²+y²+z²)^(3/2)} = x₀∫y₁y₂{R²-y²(x₀²+R²-y²)R²+x₀²}&thicksp;dy - x₀∫y₁y₂{z₁(x₀²+z₁²)x₀²+y²+z₁²}&thicksp;dy.

Das Integral ist nicht trivial. Aber man findet schliesslich einen analytischen Ausdruck. Ich gebe einige Substituionen für $arcsin$ an, damit die Lösung des Integrals etwas übersichtlicher wird.

$t$₁ = arcsin{({-x₀y₂+2x₀}+{22}} t₂ = arcsin{({-x₀y₂-2x₀}-{22}} t₃ = arcsin{({-x₀y₁+2x₀}+{22}} t₄ = arcsin{({-x₀y₁-2x₀}-{22}}

$\Omega$_β(x₀,s,n,m) = -{[{arcsin{({-y₂x₀}}2}+{t₁+t₂4}} + {[{arcsin{({-y₁x₀}}2}+{t₃+t₄4}} - arctan{({y₂ z₁x₀x₀²+y₂²+z₁²}} + arctan{({y₁ z₁x₀x₀²+y₁²+z₁²}} + Ω_α(x₀,s,ŷ₁,ŷ₂,z₁,z₂) mit&quad;y₁=max{(ŷ₁,x₀²-z₂²} und&quad;y₂=min{(ŷ₂,x₀²-z₁²} und&quad;z₂=min{(z₂,x₀²-ŷ₁²} und&quad;ŷ₁ = (2m+1)s und&quad;ŷ₂ = (2m+3)s und&quad;z₁ = (2n+1)s und&quad;z₂ = (2n+3)s.

Schliesslich lässt sich der obige Ausdruck zusammenfassend angeben als

$\Omega$_β(x₀,s) = 4∑_j=1^[k]∑₁m=[l_n-1]¹[l_n]p^(n+m)Ω_β(x₀,s,n,m) mit&quad;k={{x₀²-s²s²}+12} und&quad;n = [k]-j+1 und&quad; l_n={{x₀²-(2n-1)²s²s²}+12} mit&quad;l₀≡1.

Als nächstes werde ich die Raumwinkel $\Omega$_γ(x₀,s) und $\Omega$_δ(x₀,s) berechnen. Es handelt sich dabei bloss um zwei Spezialfälle von $\Omega$_α(x₀,s).

$\Omega$_γ(x₀,s) = Ω_α(x₀,s,n,m) mit&quad;m=0 und&quad;n=0.

$\Omega$_δ(x₀,s) = 4∑_n=1^[k]p^(n+m)Ω_α(x₀,s,n,m) mit&quad;k={{x₀²-s²s²}+12} und&quad;m=0.

Zu letzt werde ich den Raumwinkel $\Omega$_ε(x₀,s) berechnen. Analog zum vorher Gesagten handelt es sich auch hier um einen Spezialfall von $\Omega$_β(x₀,s).

$\Omega$_ε(x₀,s) = 8p^(n+m)Ω_β(x₀,s,n,m) mit&quad;n={{x₀²-s²s²}+12} und&quad;ŷ₁=0 und&quad;ŷ₂=s und&quad;m = 0

Ich kann nun endlich den gesuchten Raumwinkel $\Omega (x$₀,s) angeben

$\Omega (x$₀,s) = Ω_α(x₀,s)+Ω_β(x₀,s)+Ω_γ(x₀,s)+Ω_δ(x₀,s)+Ω_ε(x₀,s).